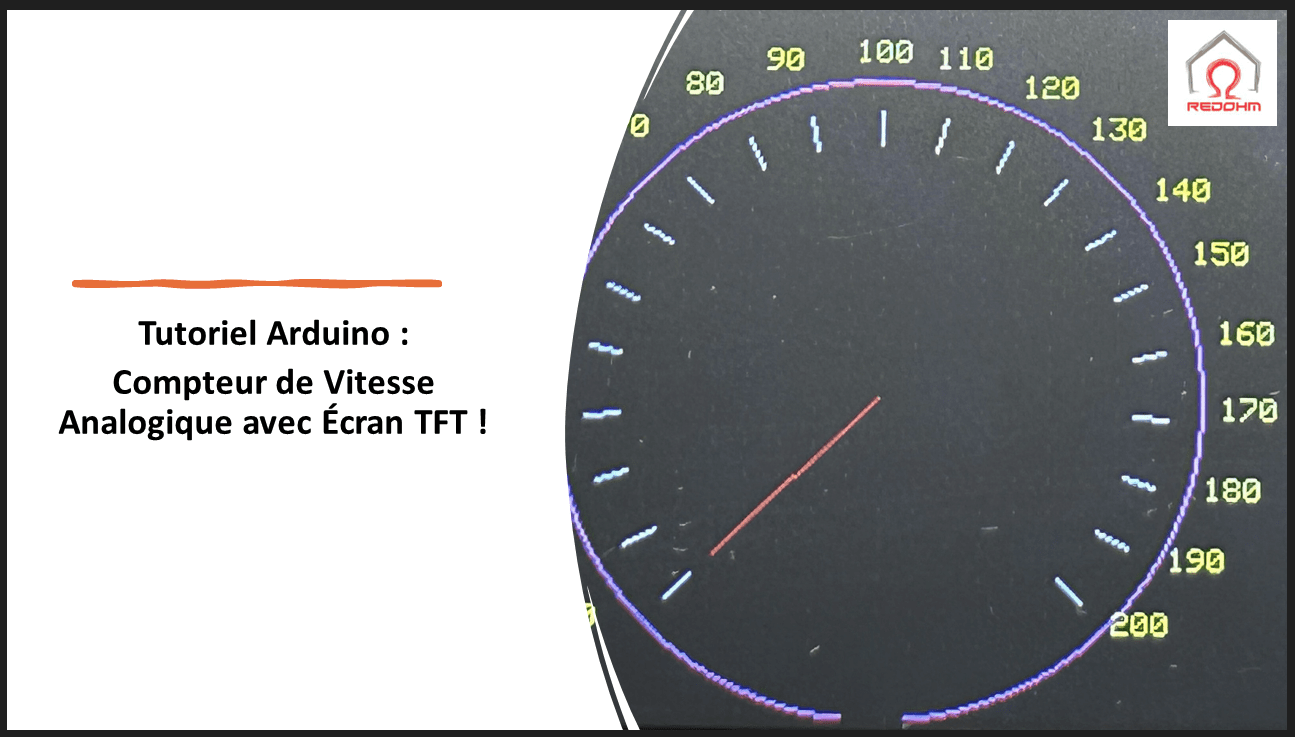
.
Ce programme est conçu pour fonctionner avec une carte Arduino et un écran TFT. Son objectif principal est d’afficher un compteur de vitesse sur l’écran TFT, simulant ainsi un tableau de bord analogique, comme celui que l’on pourrait trouver dans une voiture ou une moto.
- Fonctionnement de base :
- Le programme lit une valeur analogique (provenant d’un capteur ou d’un potentiomètre connecté à la broche A9 de l’Arduino) qui est censée représenter une vitesse.
- Cette valeur analogique est ensuite mappée (ou convertie) en une valeur de vitesse allant de 0 à une vitesse maximale définie (dans ce cas,
Vitesse_maxest définie à 150). - Le programme utilise la vitesse déduite pour ajuster une aiguille sur l’écran TFT. Cette aiguille indique la vitesse actuelle, similaire à un compteur de vitesse analogique. Outre l’aiguille, le programme affiche la vitesse exacte numériquement sur l’écran.
- Caractéristiques visuelles :
- L’écran TFT affiche un cercle représentant le compteur de vitesse, avec des marques (ou graduations) pour indiquer différentes vitesses. Ces marques sont espacées de 10 unités de vitesse et sont accompagnées de chiffres pour faciliter la lecture.
- Une aiguille pivote autour du centre du cercle, indiquant la vitesse actuelle.
- Mise à jour dynamique :
- Le programme vérifie en continu la valeur analogique lue. Il met à jour l’affichage de l’aiguille et de la valeur numérique en conséquence.
- Le programme évite les mises à jour inutiles pour réduire les clignotements sur l’écran. »Il met à jour l’affichage seulement quand la vitesse change.
Pourquoi le système de coordonnées sur un écran TFT diffère-t-il de la convention mathématique? Comment cela impacte-t-il la programmation sur ces écrans?
Lorsque nous parlons du cercle trigonométrique standard en mathématiques, il commence avec 0° à droite (sur l’axe des abscisses positif) et augmente dans le sens antihoraire.
Cependant, dans de nombreux systèmes de graphiques informatiques, y compris la plupart des écrans TFT pilotés par Arduino, le système de coordonnées est différent :
- Origine (0,0) : L’origine du système de coordonnées se trouve généralement dans le coin supérieur gauche de l’écran, et non au centre.
- Direction positive de l’axe Y : Dans la plupart des systèmes trigonométriques, l’axe Y est positif vers le haut. Mais dans de nombreux systèmes graphiques, l’axe Y est positif vers le bas.
- Sens de rotation : En trigonométrie, l’angle augmente dans le sens antihoraire. Cependant, sur les écrans TFT, c’est différent. L’axe Y positif change la direction. Les objets tournent dans le sens horaire.
Ces différences peuvent rendre la translation des concepts mathématiques trigonométriques dans le monde du graphisme informatique un peu déroutante au début. C’est pourquoi, par exemple, le cercle trigonométrique commence souvent à un angle différent, comme 135° pour le compteur dans le code que nous avons examiné, afin d’avoir le point de départ à l’endroit souhaité.
Ainsi, lors de la programmation pour des écrans TFT ou d’autres systèmes de graphiques informatiques, nous devons prendre en compte ces différences et ajuster les calculs en conséquence.
Pourquoi est-il nécessaire de convertir les degrés en radians lors de l’utilisation de fonctions trigonométriques sur Arduino?
Sur Arduino, la nécessité de traduire les degrés en radians n’est pas due à une limitation spécifique de la plate-forme Arduino elle-même, mais plutôt à la manière dont les fonctions trigonométriques standard, telles que sin() et cos(), sont définies dans la plupart des langages de programmation, y compris le C++ utilisé par l’Arduino.
Voici quelques raisons pour lesquelles les radians sont utilisés pour les fonctions trigonométriques :
Définition mathématique : En mathématiques, le radian est la mesure standard pour les angles. C’est une unité sans dimension qui représente le rapport entre la longueur d’un arc et le rayon du cercle. Cette propriété rend les radians plus fondamentaux et naturels pour décrire les angles dans le contexte des mathématiques.
Simplicité des formules : De nombreuses formules en trigonométrie, en analyse et en physique sont plus simples lorsqu’elles sont exprimées en radians. Par exemple, la dérivée de sin(x) est cos(x) seulement si x est en radians.
